The Königsberg Bridge Problem: A Journey into the Birth of Graph Theory

Related Articles: The Königsberg Bridge Problem: A Journey into the Birth of Graph Theory

Introduction

With great pleasure, we will explore the intriguing topic related to The Königsberg Bridge Problem: A Journey into the Birth of Graph Theory. Let’s weave interesting information and offer fresh perspectives to the readers.

The Königsberg Bridge Problem: A Journey into the Birth of Graph Theory

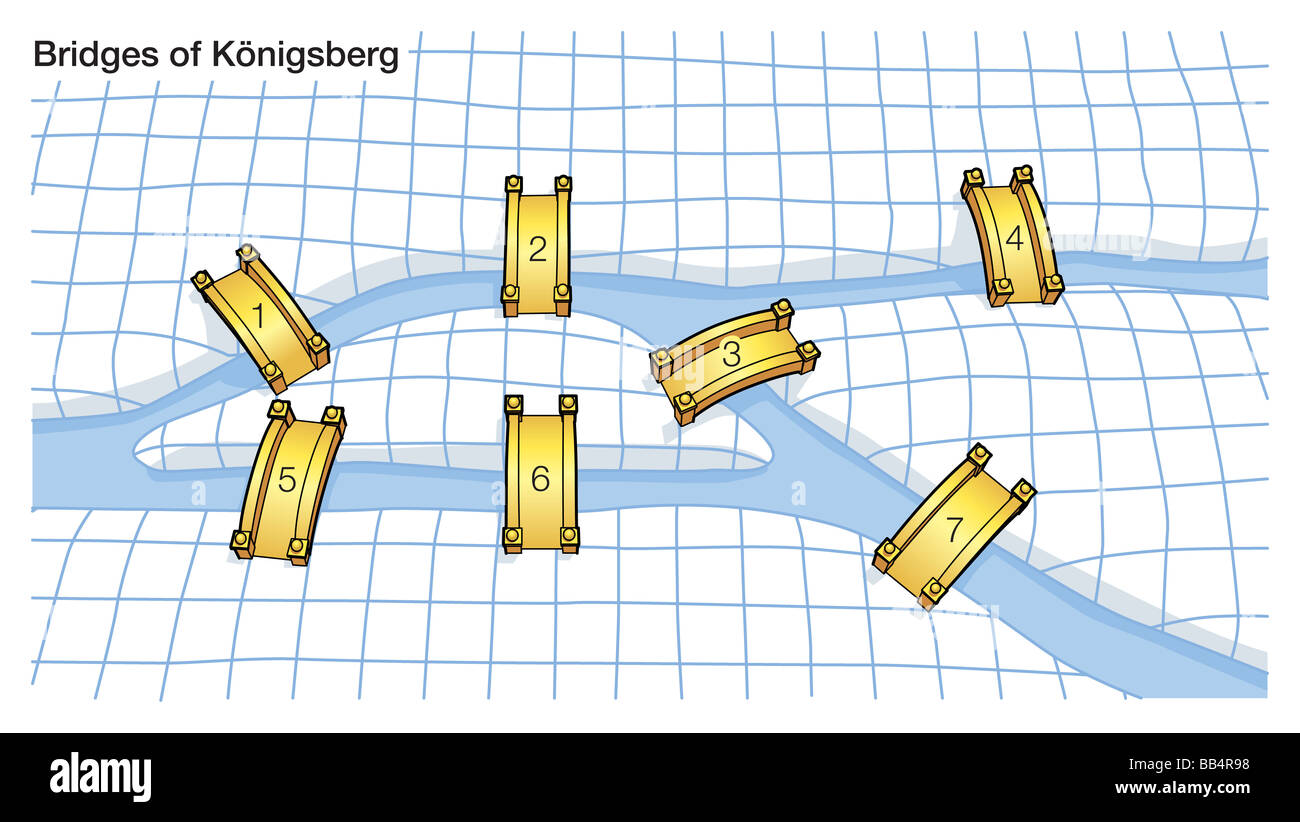
The Königsberg Bridge Problem, a seemingly simple puzzle about crossing bridges in a Prussian city, holds a profound significance in the history of mathematics. It was not simply a local curiosity, but a problem that sparked a revolution in the field, laying the foundation for a new branch of mathematics: graph theory. This article delves into the intricacies of the Königsberg Bridge Problem, exploring its historical context, its mathematical solution, and its enduring impact on the world of mathematics and beyond.

The Problem: A City Divided by Seven Bridges

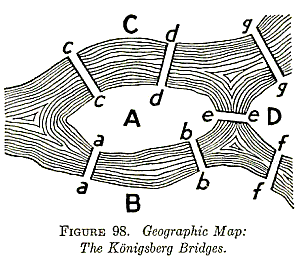
Königsberg, now Kaliningrad in Russia, was once a city divided by the Pregel River. The river flowed through the city, forming an island and two separate landmasses. Connecting these landmasses were seven bridges, a feature that intrigued the city’s residents. The challenge, as it was posed in the 18th century, was this: could a person walk through the city, crossing each bridge exactly once, and return to the starting point?

The Königsberg Bridge Problem, with its seemingly straightforward nature, captivated the minds of mathematicians and non-mathematicians alike. People tried to solve it by walking the bridges themselves, by drawing diagrams, and by using various logical arguments. However, no one could find a solution that satisfied the problem’s conditions.

Leonhard Euler: The Father of Graph Theory

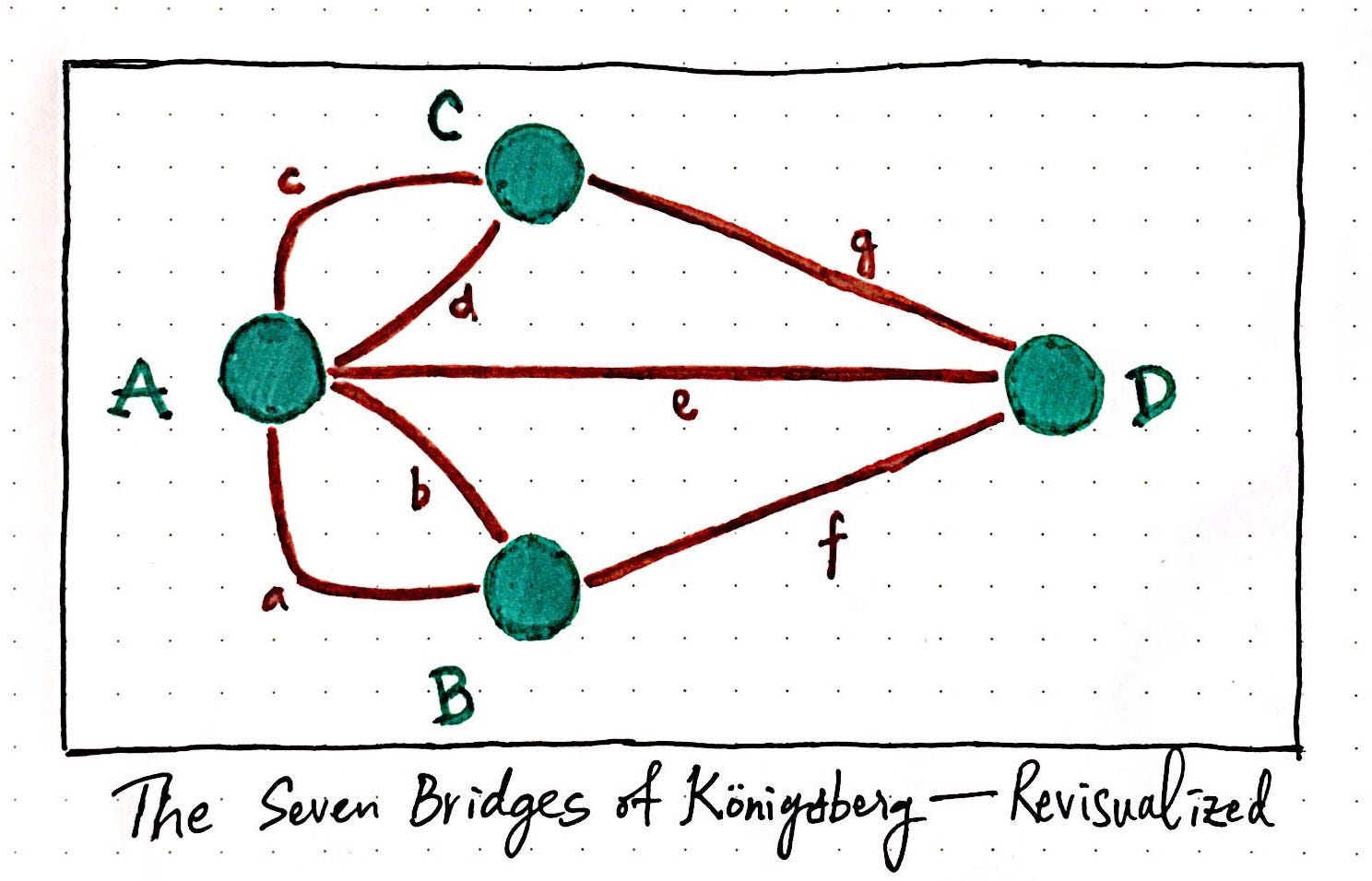
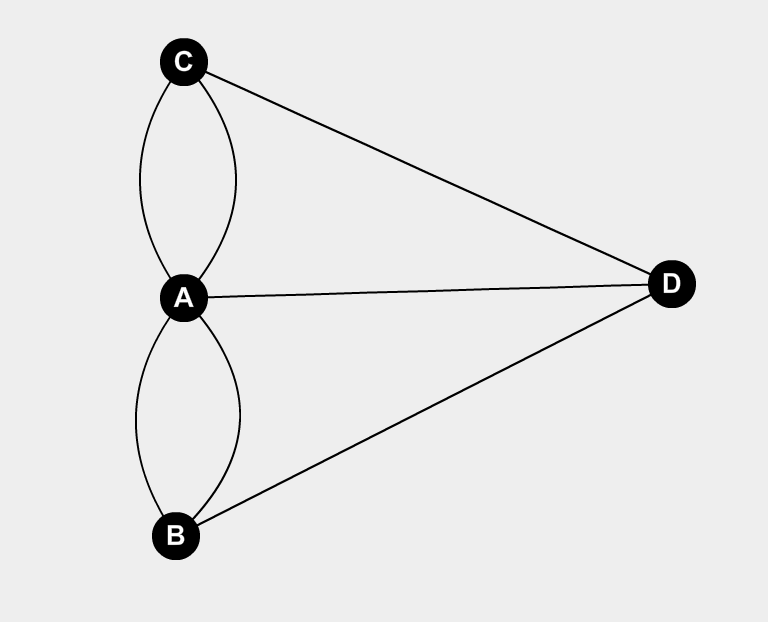
In 1736, the renowned Swiss mathematician Leonhard Euler took up the challenge. Instead of focusing on the physical bridges and the city itself, Euler saw the problem in a new light. He realized that the essential elements were the landmasses and the connections between them, not their physical attributes. This fundamental shift in perspective led to the birth of graph theory.

Euler represented the landmasses as points (vertices) and the bridges as lines connecting these points (edges). This abstract representation, now known as a graph, allowed him to analyze the problem in a more general and systematic way.

He observed that each time a person crossed a bridge, they entered and left a landmass. This meant that for every landmass, the number of bridges connected to it had to be even, except for the starting and ending points, which could have an odd number of bridges. This crucial observation, known as Euler’s theorem, became the key to solving the Königsberg Bridge Problem.

The Solution: No Single Path Possible

Applying his theorem to the Königsberg Bridge Problem, Euler found that there was no solution. Each landmass in Königsberg had an odd number of bridges connected to it, contradicting his theorem. Therefore, it was impossible to walk through the city, crossing each bridge exactly once, and returning to the starting point.

Euler’s solution, which he presented in his paper "The Seven Bridges of Königsberg," was not just a mathematical solution to a local puzzle. It marked a significant milestone in the history of mathematics, introducing the concept of graph theory and its powerful applications.

The Impact: A Revolution in Mathematics and Beyond

Graph theory, born out of the Königsberg Bridge Problem, has since become a fundamental branch of mathematics with vast applications in various fields. It is used to model and analyze networks, such as social networks, computer networks, and transportation networks.

Here are some examples of its applications:

• Computer Science: Graph theory is used in designing algorithms for routing information in computer networks, searching for optimal paths in GPS systems, and analyzing social networks.
• Biology: It helps in understanding the structure of molecules, mapping genetic networks, and analyzing the spread of diseases.
• Operations Research: Graph theory is used to optimize logistics, schedule tasks, and manage resources.
• Social Sciences: It helps in understanding social interactions, analyzing voting patterns, and studying the spread of information.

The Königsberg Bridge Problem, therefore, has had a lasting impact on mathematics and beyond. It has not only shaped the development of graph theory but also influenced numerous fields that rely on network analysis and optimization.

FAQs: Exploring the Königsberg Bridge Problem Further

Q: What is the difference between a graph and a map?

A: A map is a visual representation of a physical space, typically showing geographical features like roads, buildings, and rivers. A graph, on the other hand, is an abstract representation of relationships between objects, focusing on connections rather than physical locations. In the Königsberg Bridge Problem, the map of Königsberg is the physical representation, while the graph is the abstract representation of the landmasses and bridges.

Q: What is the difference between a simple graph and a multigraph?

A: In a simple graph, there is only one edge connecting any two vertices. In a multigraph, multiple edges can connect the same pair of vertices. The Königsberg Bridge Problem is represented by a multigraph because there are multiple bridges connecting some of the landmasses.

Q: How does Euler’s theorem apply to other networks?

A: Euler’s theorem, which states that a graph can be traversed by crossing each edge exactly once and returning to the starting point only if all vertices have an even degree (number of edges connected to them), applies to any network that can be represented as a graph. For example, it can be used to determine if a network of roads can be traversed without repeating any road segment.

Q: What are some other famous problems in graph theory?

A: Besides the Königsberg Bridge Problem, other famous problems in graph theory include the Traveling Salesperson Problem, the Four Color Theorem, and the Hamiltonian Cycle Problem. These problems have significant applications in various fields and continue to inspire research in graph theory.

Tips: Exploring the Königsberg Bridge Problem Further

• Visualize the problem: Draw a simple diagram of the Königsberg bridges and landmasses. This will help you understand the problem and its solution visually.
• Explore Euler’s theorem: Read more about Euler’s theorem and its applications in graph theory. You can find numerous resources online and in textbooks.
• Explore other graph theory problems: Research other famous problems in graph theory, such as the Traveling Salesperson Problem or the Four Color Theorem. This will give you a broader understanding of the field.
• Connect graph theory to real-world applications: Think about how graph theory is used in different fields, such as computer science, biology, and social sciences. This will help you appreciate the practical value of graph theory.

Conclusion: A Legacy of Innovation

The Königsberg Bridge Problem, a seemingly simple puzzle about crossing bridges in a Prussian city, led to the birth of graph theory, a fundamental branch of mathematics with vast applications in various fields. Euler’s solution, which demonstrated the impossibility of traversing the city under the given conditions, marked a significant milestone in the history of mathematics, paving the way for the development of a powerful tool for analyzing networks and relationships.

From understanding social networks to optimizing logistics, graph theory continues to influence our world, all thanks to the legacy of a seemingly simple problem about bridges in Königsberg. The problem, which once puzzled the city’s residents, has become a timeless testament to the power of mathematical thinking and its ability to solve complex problems and drive innovation in various fields.

Closure

Thus, we hope this article has provided valuable insights into The Königsberg Bridge Problem: A Journey into the Birth of Graph Theory. We hope you find this article informative and beneficial. See you in our next article!