Unlocking the Power of Boolean Logic: A Comprehensive Guide to Karnaugh Maps with Four Variables

Related Articles: Unlocking the Power of Boolean Logic: A Comprehensive Guide to Karnaugh Maps with Four Variables

Introduction

With great pleasure, we will explore the intriguing topic related to Unlocking the Power of Boolean Logic: A Comprehensive Guide to Karnaugh Maps with Four Variables. Let’s weave interesting information and offer fresh perspectives to the readers.

Unlocking the Power of Boolean Logic: A Comprehensive Guide to Karnaugh Maps with Four Variables

In the realm of digital electronics, Boolean algebra serves as the fundamental language for representing and manipulating logical relationships. This language, with its inherent simplicity and power, underpins the design and operation of countless electronic circuits. One of the most effective tools for simplifying Boolean expressions and optimizing circuit designs is the Karnaugh map, particularly when dealing with a small number of variables.

This article delves into the intricacies of Karnaugh maps, specifically focusing on their application with four variables. We will explore the construction, interpretation, and utilization of these maps, highlighting their crucial role in simplifying Boolean expressions and ultimately optimizing circuit design.

Understanding the Basics: A Foundation for Karnaugh Maps

Before diving into the specifics of four-variable Karnaugh maps, it is essential to grasp the underlying principles that govern their operation.

Boolean Algebra: The Language of Logic

Boolean algebra, named after the mathematician George Boole, provides a framework for representing and manipulating logical relationships. It utilizes binary values, represented by 0 and 1, to denote "false" and "true," respectively. Boolean expressions combine these values using logical operators such as AND, OR, and NOT.

Truth Tables: Mapping Logical Relationships

Truth tables provide a systematic way to represent the output of a Boolean expression for all possible combinations of input values. Each row in a truth table corresponds to a unique combination of input values, and the corresponding output value is listed in the final column.

Minimization: The Quest for Efficiency

In digital circuit design, minimizing the number of logic gates required to implement a Boolean expression is crucial for achieving optimal performance and cost-effectiveness. This minimization process aims to reduce the complexity of the circuit while preserving its functionality.

Constructing the Four-Variable Karnaugh Map: A Visual Representation of Boolean Logic

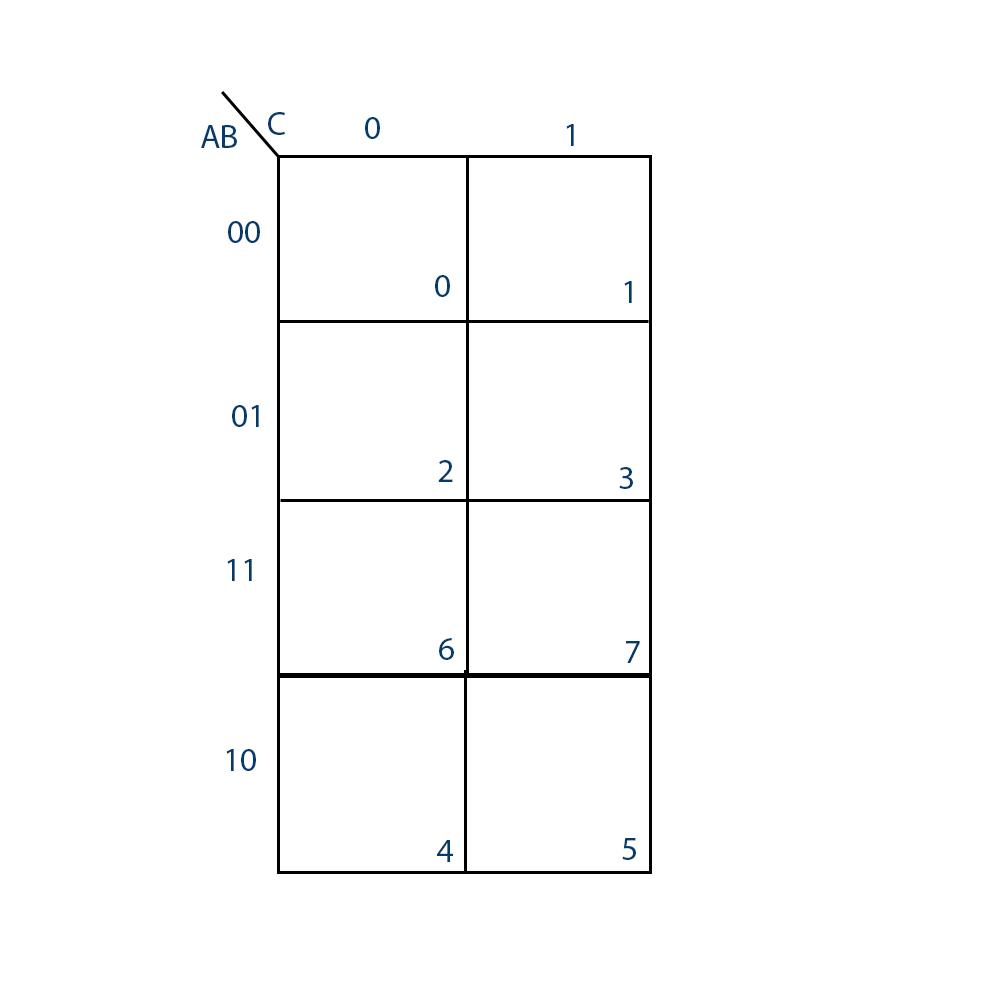
The Karnaugh map, named after Maurice Karnaugh, provides a visual representation of a Boolean expression, making it easier to identify patterns and simplify the expression. For four variables, the Karnaugh map consists of a 2×4 grid, with each cell representing a unique combination of input values.

The Grid Structure:

The grid is divided into four rows and two columns. Each row represents a specific combination of the two most significant input variables, while each column represents a specific combination of the two least significant input variables.

Cell Assignment:

Each cell in the Karnaugh map is assigned a unique combination of input values. The binary representation of these input values determines the cell’s position within the grid.

Adjacent Cells:

Crucially, adjacent cells in the Karnaugh map differ in only one input variable. This adjacency property is fundamental for simplifying Boolean expressions.

Example: A Four-Variable Karnaugh Map

Consider a Boolean expression with four input variables: A, B, C, and D. The corresponding Karnaugh map would be structured as follows:

CD	00	01	11	10
00
01
11
10

Each cell in the map would be assigned a unique combination of input values, for example, the top-left cell would correspond to A=0, B=0, C=0, and D=0, while the bottom-right cell would correspond to A=1, B=1, C=1, and D=0.

Populating the Karnaugh Map: Mapping Truth Tables to Visual Representations

Once the Karnaugh map is constructed, the next step is to populate it with the output values from the corresponding truth table.

Mapping Output Values:

For each row in the truth table, the corresponding output value is entered into the cell that represents the same combination of input values.

Example: Populating the Karnaugh Map

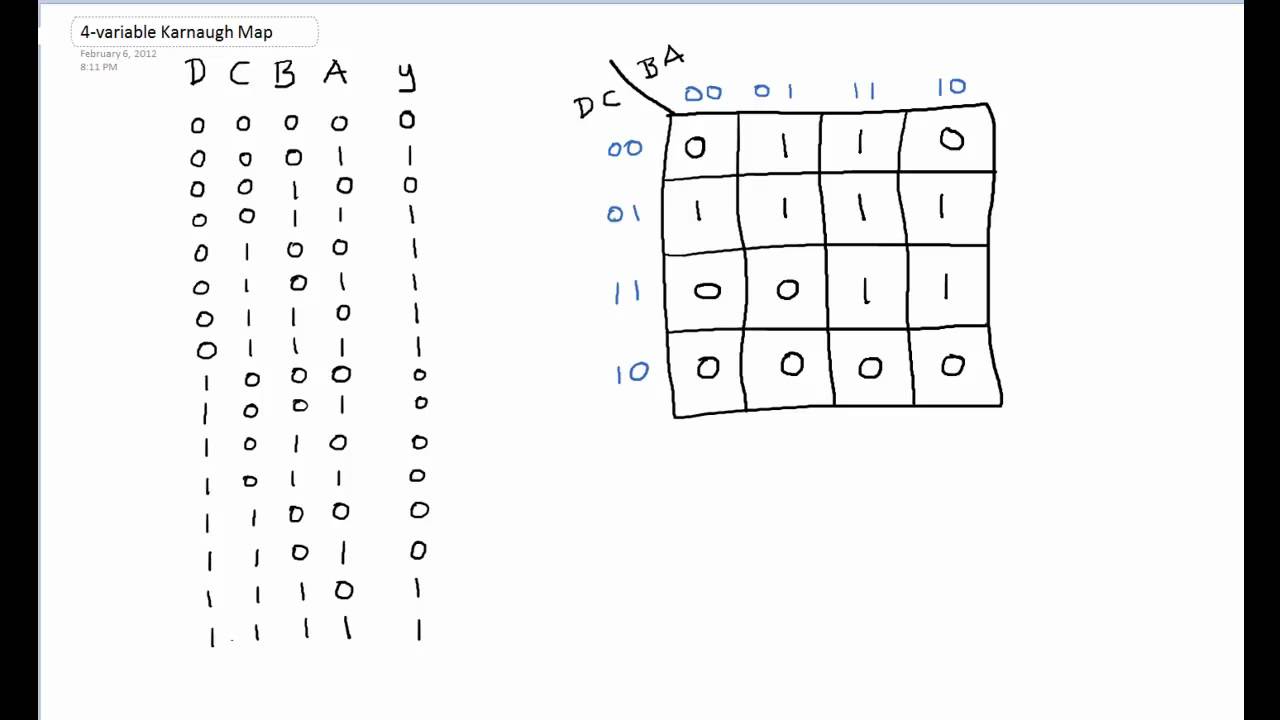
Let’s assume we have a truth table for a Boolean expression with four input variables (A, B, C, D) and one output variable (F). The truth table is as follows:

A	B	C	D	F
0	0	0	0	1
0	0	0	1	0
0	0	1	0	1
0	0	1	1	1
0	1	0	0	0
0	1	0	1	1
0	1	1	0	0
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	0
1	0	1	1	1
1	1	0	0	0
1	1	0	1	0
1	1	1	0	1
1	1	1	1	0

Using this truth table, we can populate the Karnaugh map. For example, the first row of the truth table (A=0, B=0, C=0, D=0, F=1) corresponds to the top-left cell in the Karnaugh map, where we would enter the output value ‘1’.

Simplifying Boolean Expressions: Uncovering Patterns and Reducing Complexity

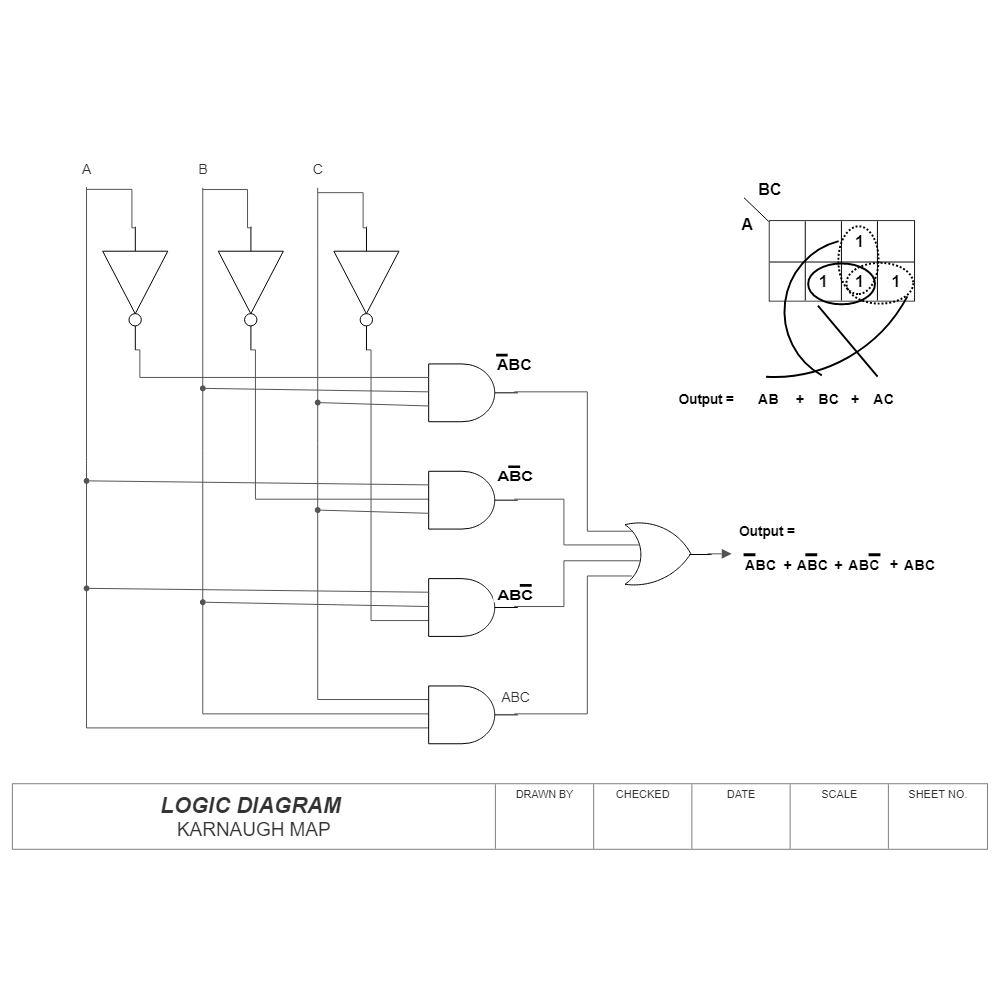
The Karnaugh map’s true power lies in its ability to simplify Boolean expressions by visually identifying patterns and grouping adjacent cells with the same output value.

Grouping Adjacent Cells:

Adjacent cells in the Karnaugh map, differing in only one input variable, can be grouped together. These groups can be rectangular or square, and they should be as large as possible.

Identifying Essential Prime Implicants:

Each group represents a product term in the simplified Boolean expression. The goal is to find the smallest set of groups that cover all the ‘1’ cells in the Karnaugh map. These groups are called essential prime implicants.

Example: Simplifying a Boolean Expression

Let’s consider the Karnaugh map populated with the output values from the previous example.

CD	00	01	11	10
00	1	0	1	1
01	0	1	0	1
11	1	0	1	0
10	0	0	0	0

We can identify three groups in this map:

• Group 1: Cells with input values (A=0, B=0, C=0, D=0) and (A=0, B=0, C=1, D=0) – this group corresponds to the product term !A!B!D.
• Group 2: Cells with input values (A=0, B=0, C=1, D=1) and (A=1, B=0, C=1, D=1) – this group corresponds to the product term !B!C.
• Group 3: Cells with input values (A=1, B=0, C=0, D=0) and (A=1, B=0, C=1, D=0) – this group corresponds to the product term !B!D.

These three groups cover all the ‘1’ cells in the Karnaugh map, and they are the essential prime implicants. Therefore, the simplified Boolean expression for the original truth table is:

F = !A!B!D + !B!C + !B!D

Advantages of Using Karnaugh Maps: Optimizing Circuit Design and Simplifying Boolean Expressions

Karnaugh maps offer several key advantages for simplifying Boolean expressions and optimizing circuit design:

• Visual Simplification: They provide a visual representation of Boolean expressions, making it easier to identify patterns and simplify the expression.
• Minimized Logic Gates: By identifying essential prime implicants, Karnaugh maps help minimize the number of logic gates required to implement the expression, resulting in more efficient and cost-effective circuits.
• Reduced Circuit Complexity: Simplified Boolean expressions translate to simpler and more compact circuits, reducing the overall complexity of the design.
• Improved Performance: Reduced circuit complexity leads to improved performance, as the signal propagation delay is reduced.
• Enhanced Readability: Karnaugh maps offer a more intuitive and readable representation of Boolean expressions compared to traditional algebraic methods.

FAQs: Addressing Common Questions about Karnaugh Maps with Four Variables

1. How do I handle "don’t care" conditions in a four-variable Karnaugh map?

"Don’t care" conditions occur when the output value for a specific combination of input values is irrelevant to the circuit’s functionality. In a Karnaugh map, these conditions are represented by the symbol ‘X’. When simplifying the expression, "don’t care" conditions can be treated as either ‘0’ or ‘1’, depending on which choice leads to a larger group and a simpler expression.

2. What are some common mistakes to avoid when using Karnaugh maps?

• Incorrectly Grouping Cells: Ensure that groups are rectangular or square and include only adjacent cells.
• Missing Essential Prime Implicants: Carefully identify all essential prime implicants to ensure a complete simplification of the expression.
• Overlapping Groups: Avoid creating overlapping groups, as this can lead to redundancy in the simplified expression.
• Ignoring "Don’t Care" Conditions: Utilize "don’t care" conditions strategically to achieve a more simplified expression.

3. Can Karnaugh maps be used for more than four variables?

While Karnaugh maps are highly effective for up to four variables, their visual representation becomes increasingly complex and difficult to manage with more variables. For five or more variables, alternative methods such as Quine-McCluskey minimization are typically employed.

4. What are the limitations of Karnaugh maps?

• Limited Number of Variables: As mentioned above, Karnaugh maps are most effective for up to four variables. Beyond that, they become unwieldy.
• Complexity for Large Expressions: For complex expressions with numerous input variables, even four-variable Karnaugh maps can become difficult to manage and interpret.
• Lack of Automation: Unlike other minimization techniques, Karnaugh maps rely heavily on manual analysis and grouping, which can be time-consuming and prone to errors.

Tips for Effective Karnaugh Map Usage: Mastering the Art of Boolean Simplification

• Start with a Clear Truth Table: Ensure the truth table accurately reflects the desired functionality of the circuit.
• Organize the Karnaugh Map: Carefully assign input values to cells, ensuring correct adjacency relationships.
• Identify Essential Prime Implicants: Thoroughly analyze the map to identify all essential prime implicants, avoiding unnecessary groups.
• Utilize "Don’t Care" Conditions: Strategically incorporate "don’t care" conditions to achieve a more simplified expression.
• Verify the Result: After simplifying the expression, verify the result by comparing it to the original truth table.

Conclusion: Embracing the Power of Karnaugh Maps for Optimized Circuit Design

Karnaugh maps provide a powerful and intuitive method for simplifying Boolean expressions and optimizing digital circuit design. By visually representing the relationships between input and output values, Karnaugh maps enable efficient identification of patterns and grouping of adjacent cells, leading to simplified expressions and more efficient circuits. While they are most effective for up to four variables, Karnaugh maps remain a valuable tool for designers seeking to optimize their circuits and enhance their understanding of Boolean logic.

Closure

Thus, we hope this article has provided valuable insights into Unlocking the Power of Boolean Logic: A Comprehensive Guide to Karnaugh Maps with Four Variables. We appreciate your attention to our article. See you in our next article!