Unveiling the Chaos: A Deep Dive into the Hénon Map

Related Articles: Unveiling the Chaos: A Deep Dive into the Hénon Map

Introduction

With great pleasure, we will explore the intriguing topic related to Unveiling the Chaos: A Deep Dive into the Hénon Map. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Chaos: A Deep Dive into the Hénon Map

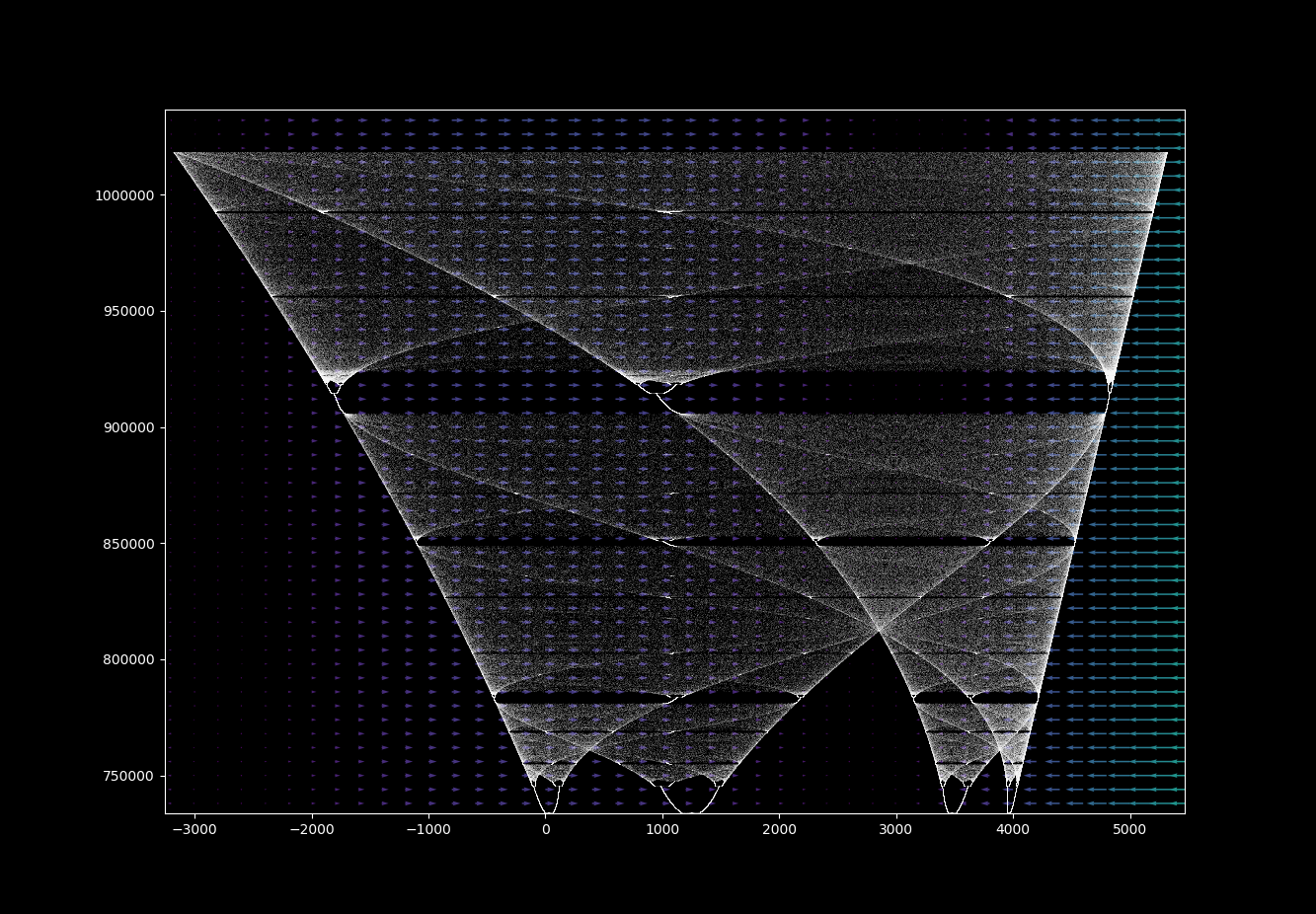
The realm of mathematics often reveals intricate patterns and surprising complexities. Among these, the Hénon map stands out as a captivating example of a seemingly simple system capable of generating profound and unpredictable behavior. This mathematical tool, introduced by Michel Hénon in 1976, offers a window into the fascinating world of chaos theory, providing a tangible illustration of how seemingly random and unpredictable behavior can arise from deterministic systems.

Understanding the Hénon Map: A Visual Journey

The Hénon map is a two-dimensional discrete dynamical system, meaning it iterates a set of equations to generate a sequence of points. The equations governing this iteration are:

• *x(n+1) = 1 – a x(n)^2 + y(n)**
• *y(n+1) = b x(n)**

Where:

• x(n) and y(n) represent the coordinates of a point at the nth iteration.
• a and b are parameters that control the behavior of the system.

The beauty of the Hénon map lies in its ability to generate a wide range of patterns, from simple periodic orbits to intricate fractal structures, depending on the chosen parameter values.

Visualizing the Hénon Map: A Tapestry of Chaos

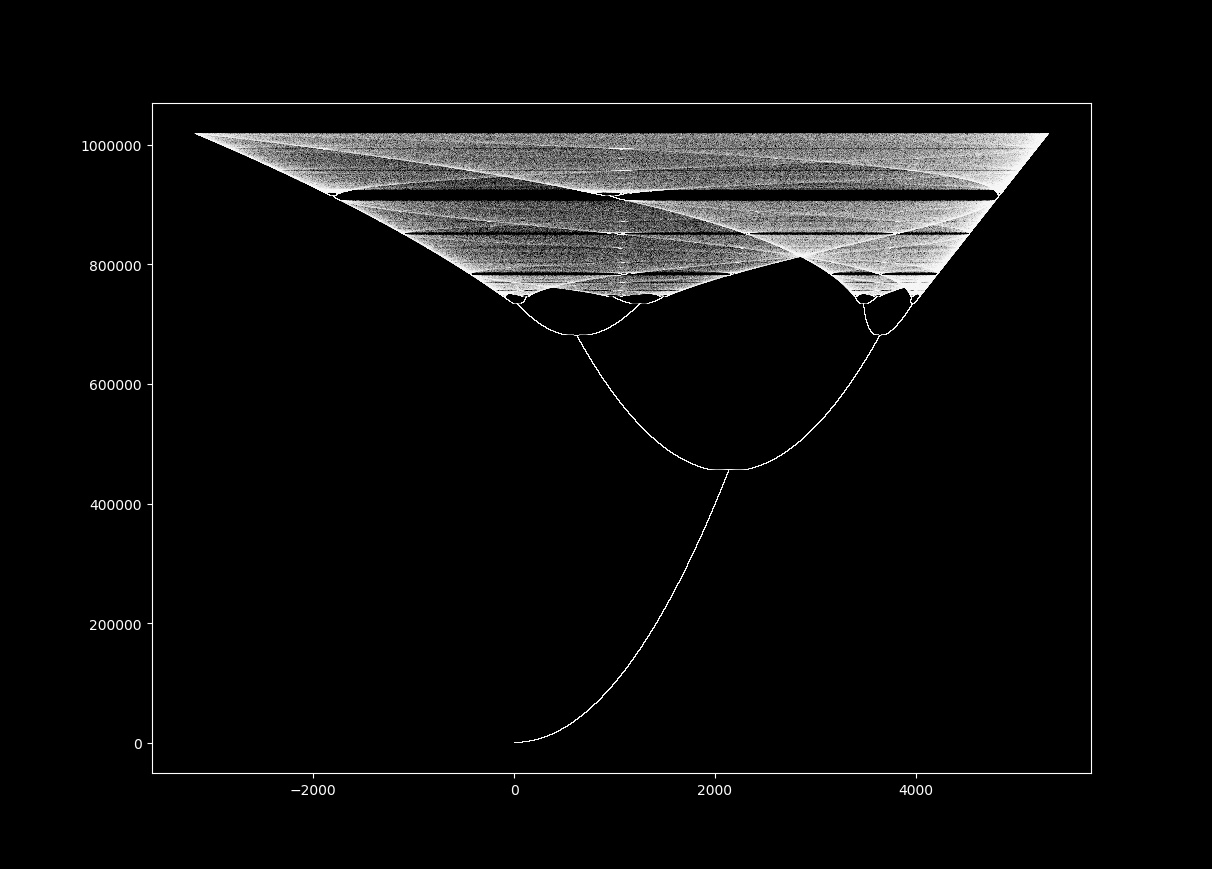
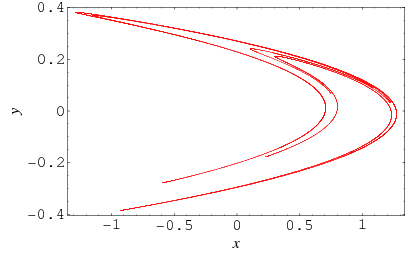
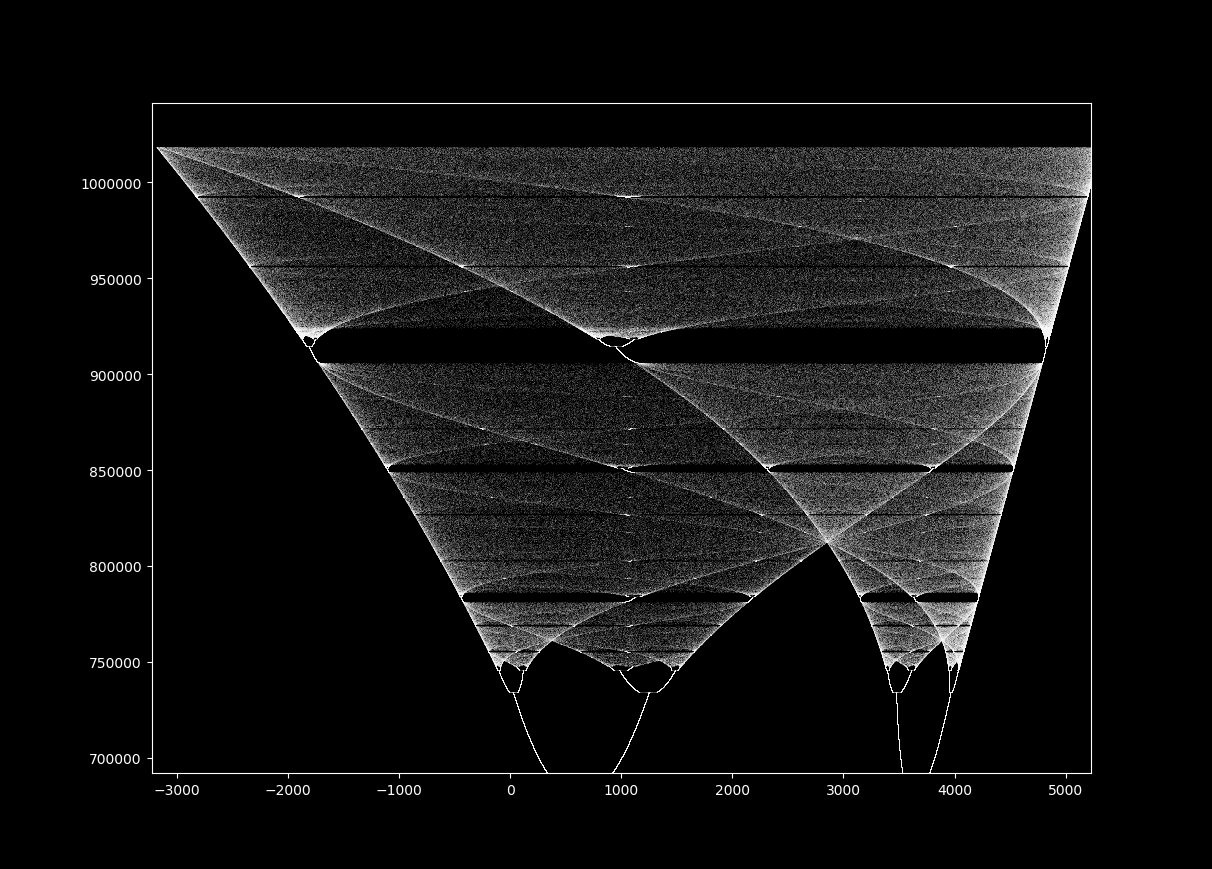
To visualize the Hénon map, one plots the sequence of points generated by the iteration. The resulting pattern, known as a "Hénon attractor," reveals the system’s dynamics. For certain parameter values, the attractor exhibits a remarkably complex structure, resembling a strange and captivating fractal.

The Significance of the Hénon Map: Unlocking the Secrets of Chaos

The Hénon map has profound implications in various fields, including:

• Chaos Theory: It serves as a fundamental model for studying chaotic systems, revealing how seemingly random behavior can emerge from deterministic equations.
• Nonlinear Dynamics: The map showcases the intricate interplay of nonlinearity, feedback, and sensitivity to initial conditions, key characteristics of complex systems.
• Fractals and Self-Similarity: The Hénon attractor exhibits fractal properties, demonstrating how complex patterns can emerge from simple rules.
• Physics and Engineering: The map finds applications in modeling various physical phenomena, such as turbulent fluid flow and chaotic oscillators.
• Biology and Ecology: The map can be used to study population dynamics, predator-prey interactions, and other complex ecological systems.

Exploring the Hénon Map: A Journey into the Unknown

The Hénon map offers a fascinating playground for exploration. Here are some key aspects to consider:

• Parameter Dependence: The behavior of the Hénon map is highly sensitive to the values of its parameters. Slight changes in ‘a’ and ‘b’ can drastically alter the resulting attractor, transitioning from simple periodic orbits to intricate chaotic patterns.
• Sensitivity to Initial Conditions: The map exhibits the characteristic "butterfly effect" of chaotic systems. Even infinitesimal differences in the initial point can lead to vastly different trajectories over time, highlighting the inherent unpredictability of chaotic systems.
• Fractal Nature: The Hénon attractor displays self-similarity, meaning that parts of the attractor resemble the whole structure at different scales. This fractal nature adds to the complexity and beauty of the map’s dynamics.

Frequently Asked Questions about the Hénon Map

1. What is the significance of the Hénon map in the context of chaos theory?

The Hénon map is a foundational model in chaos theory, demonstrating how seemingly random behavior can arise from deterministic systems. It highlights the importance of nonlinearity, feedback, and sensitivity to initial conditions in generating chaotic dynamics.

2. How does the Hénon map relate to fractals?

The Hénon attractor exhibits fractal properties, meaning that parts of the attractor resemble the whole structure at different scales. This self-similarity is a characteristic feature of fractals, making the Hénon map a valuable tool for studying these complex geometric objects.

3. What are some practical applications of the Hénon map?

The Hénon map finds applications in various fields, including modeling turbulent fluid flow, chaotic oscillators, population dynamics, and predator-prey interactions. It serves as a powerful tool for understanding complex systems in diverse scientific domains.

4. How does the Hénon map demonstrate the "butterfly effect"?

The Hénon map exhibits extreme sensitivity to initial conditions, meaning that tiny changes in the starting point can lead to drastically different trajectories over time. This illustrates the "butterfly effect," where small disturbances can have significant and unpredictable consequences in chaotic systems.

Tips for Exploring the Hénon Map

• Experiment with different parameter values: Vary the parameters ‘a’ and ‘b’ to observe how the attractor changes. You can use online tools or programming languages to generate and visualize the map.
• Focus on the initial conditions: Explore how different starting points affect the long-term behavior of the system. This will illustrate the sensitivity to initial conditions characteristic of chaotic systems.
• Study the fractal nature: Analyze the self-similarity of the Hénon attractor at different scales. This will provide insights into the intricate geometric structure of the map’s dynamics.
• Connect the map to real-world phenomena: Explore how the Hénon map can be used to model various physical, biological, or ecological systems. This will deepen your understanding of its practical applications.

Conclusion

The Hénon map is a powerful tool for exploring the fascinating realm of chaos theory. Its ability to generate intricate and unpredictable patterns from simple equations makes it a captivating example of how seemingly random behavior can emerge from deterministic systems. Whether used to illustrate the principles of chaos, study fractals, or model complex systems, the Hénon map continues to inspire and challenge our understanding of the world around us. As we continue to delve deeper into the intricacies of this mathematical tool, we uncover new insights into the profound nature of chaos and the beauty of complexity in our universe.

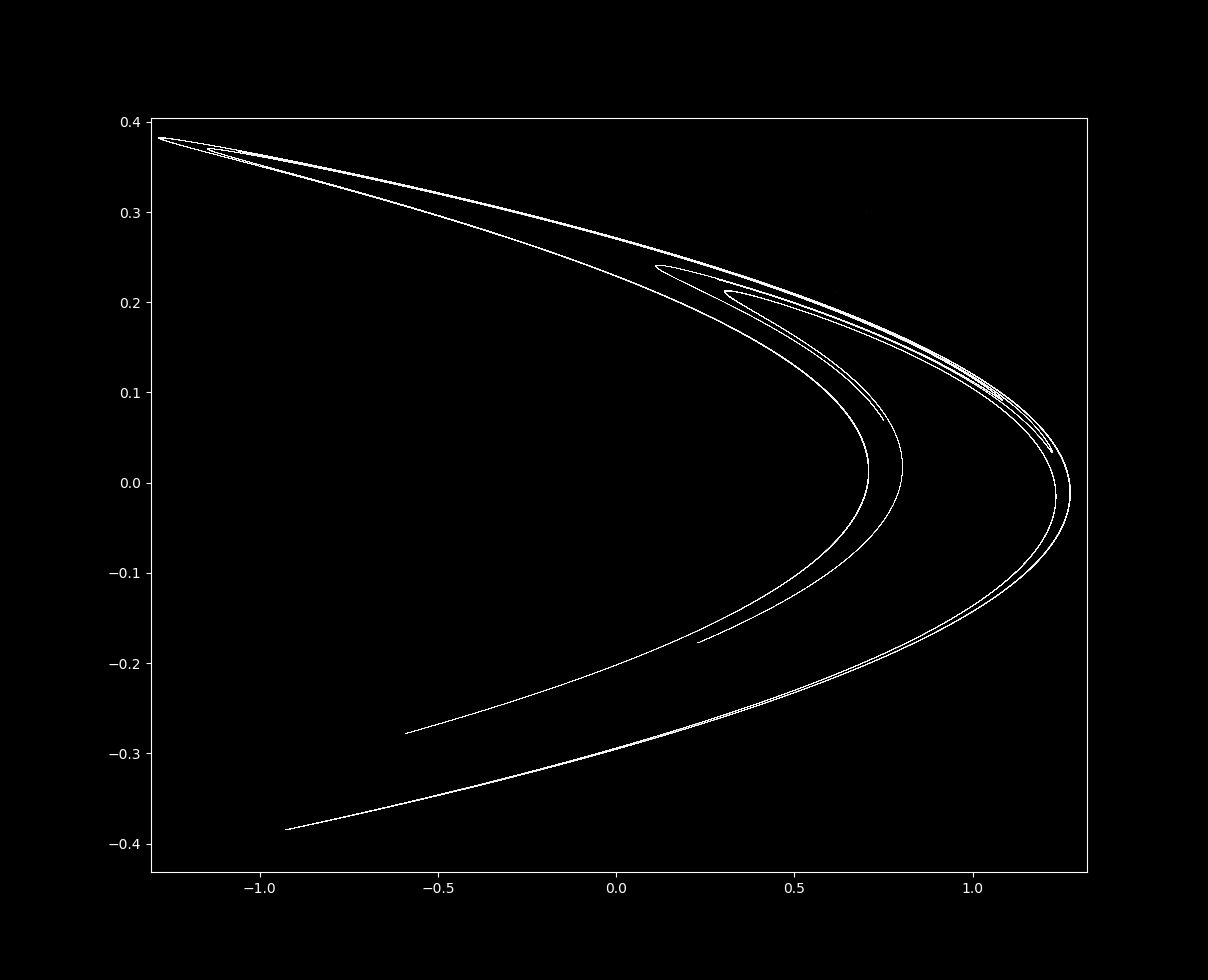
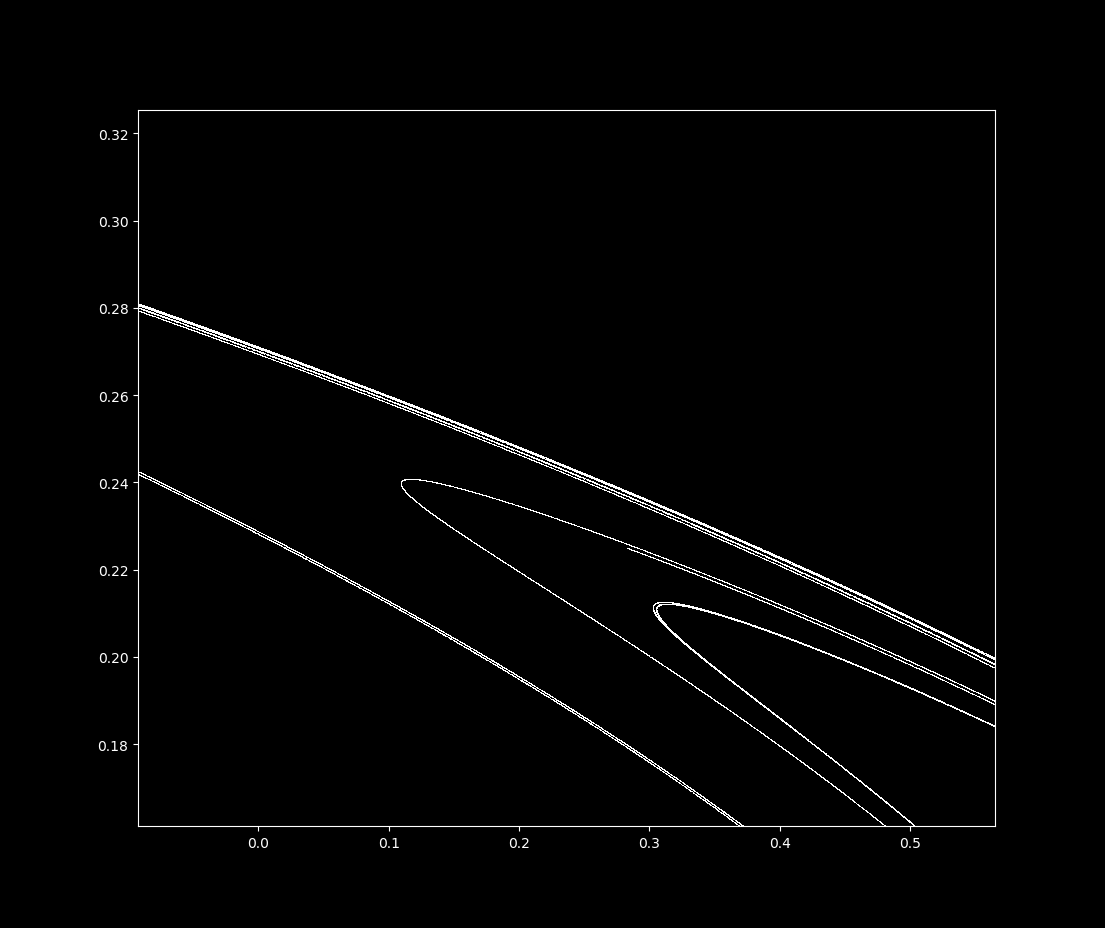
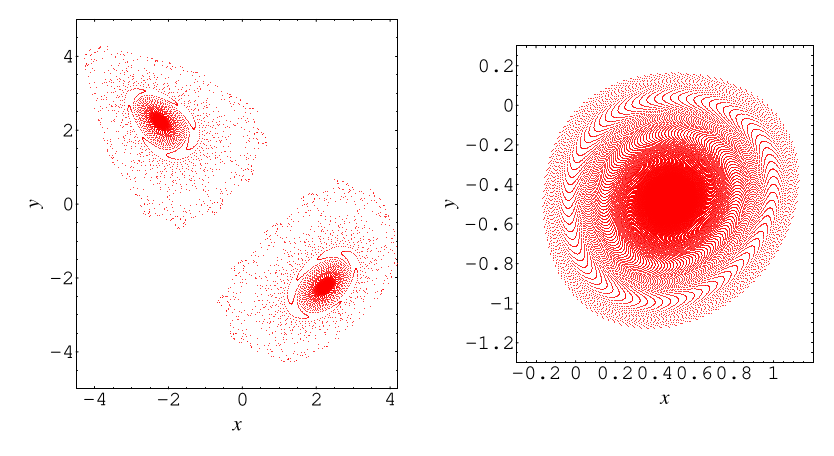
Closure

Thus, we hope this article has provided valuable insights into Unveiling the Chaos: A Deep Dive into the Hénon Map. We appreciate your attention to our article. See you in our next article!